由于计算机内只有高低电平，只能代表0和1两种状态，就此产生了二进制，而人们习惯的数字是十进制。所以就存在十进制与二进制之间的转换，但是由于二进制表示数据起来不方面（特别是当数值比较大时），十进制转换为二进制又比较麻烦，就产生了八进制、十六进制

进制对照表

img

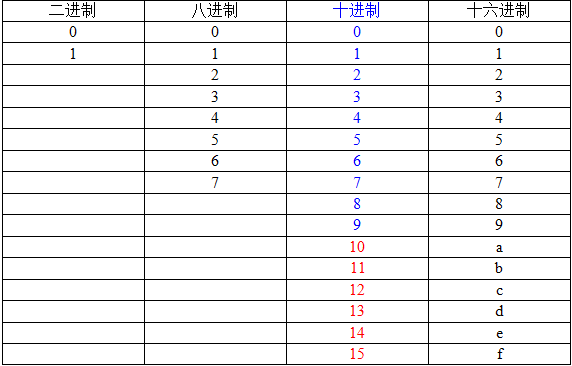
二进制/八进制/十六进制转换为十进制

二进制、八进制、十六进制转换为十进制是比较容易的

每个进制都是的每一位都是有位权重的

如：

1001（二进制） 2^31 + 2^20 + 2^10 + 2^01 = 9

1001（八进制） 8^31 + 8^20 + 8^10 + 8^01 = 513

1001（十进制） 10^31 + 10^20 + 10^10 + 10^01 = 1001

1001（十六进制） 16^31 + 16^20 + 16^10 + 16^01 = 4097

以上的都是换算到十进制的计算结果。可见同一个数字如果为不同数制大多数情况下表示的数值大小是不同的

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

#include<stdio.h>
#define Binary  0b100
#define Octal   0100
#define Decimal 100
#define Hex     0x100
int main()
{
        printf("the Binary  %d\n", Binary);
        printf("the Octal   %d\n", Octal);
        printf("the Decimal %d\n", Decimal);
        printf("the Hex     %d\n", Hex);
        return 0;
}

运行结果：

1
2
3
4

the Binary  4
the Octal  64
the Decimal 100
the Hex   256

C语言中默认数值是十进制，如果一个数值是0开头的就是八进制，如果以0x或者0X开头就是十六进制

同样可以通过printf指定不同的格式打印相应的进制

  • %d %u有无符号十进制打印

  • %o 八进制打印

  • %x %X 十六进制打印，两者区别x约定使用abcedf,而X预定使用ABCDEF

十进制到二进制快/八进制/十六进制转换

十进制 ——> 二进制

这里可以用十六进制过度。16 ，256 ，4096 ，65536 ，1048576 ，16777216 …(分别是就是16^1 ，16^2 ，16^3……) 先找第一个比要转的那个数小的数,然后用这个数除那个要转的数,得到的商就是那个位的数(位数就是是指数),然后找到第一个比余数小的数,)

如：

9999 —-> 二进制？

9999/4096 商为2，说明十六进制的第3位为2，余数为1807。

1807/256 商为7，说明十六进制的第2位为5，余数为15。

后面的直接是十六进制第一位为0，第零位为15

9999（十进制） —-> 270f（十六进制） —–> 0010 0111 0000 1111（二进制）

这样就比9999这么大的数一直除2快许多了

十进制转八进制、十六进制和上面的一样，只是省去了转换为二进制的步骤

二进制与八进制/十六进制转换

比较简单，因为分别是2的3次方，4次方。可以用3位二进制表示一位八进制，用4位二进制表示1位十六进制

0 1 2 3 4 5 6 7
000 001 010 011 100 101 110 111
0 1 2 3 4 5 6 7 8 9 a b c d e f
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

比如：

1100（二进制） —–> 001 100 —-> 14（八进制）

1100（二进制） —–> 1100 —-> c （十六进制）

反之也是一样

有符号类型的二进制

以char类型为例，负数用二进制补码表示，二进制最高位为符号位或负权

二进制 0000 0000 ~ 1111 1111

正数 0000 0000 ~ 0111 1111 0 ~ 127

负数 1000 0000 ~ 1111 1111 -128 ~ -1

原码、反码、补码

原码、反码和补码是计算机中用来表示有符号整数的编码方式。

  1. 原码（Sign-Magnitude）：原码的表示方法是将整数的符号位和数值位分开，符号位用0表示正数，用1表示负数，数值位表示整数的绝对值。例如，+5的原码为00000101，-5的原码为10000101。

  2. 反码（Ones’ Complement）：反码的表示方法是将整数的原码按位取反，即0变为1，1变为0。符号位不变。例如，+5的反码为00000101，-5的反码为11111010。

  3. 补码（Two’s Complement）：补码的表示方法是在反码的基础上加1。符号位不变。补码的一个重要特点是，对于任意一个补码，其相反数的补码等于对其按位取反后再加1。例如，+5的补码为00000101，-5的补码为11111011。

作用：

  • 原码可以直观地表示整数的符号和数值，但在进行加减运算时需要考虑符号位的处理，不利于计算机进行运算。
  • 反码在进行加减运算时，符号位的处理更加简单，但存在正零和负零的问题，且加法和减法的运算规则不一致。
  • 补码是计算机中最常用的表示有符号整数的方式。补码的加法运算与无符号数的加法运算一致，且不存在正零和负零的问题。补码还能够很方便地实现溢出和进位的处理。

总而言之，补码是计算机中表示有符号整数的标准方式，可以进行简单且一致的加减运算。

以-100的原码、反码、补码为例：

原码 1110 0100

反码 1001 1011

补码 1001 1100 （计算机实际存储的值）

负数的二进制与十进制转换

如何得出负数二进制和十进制的对应关系？有两种方式

  • 除符号位外，各位取反加1

    1111 1111

    x000 0000

    x000 0001 —-> -1

  • 把符号位看作负权-2^7

    1111 1111

    = -2^7 + 2^6 … + 2^0

    = -1

如何表示负数是人为规定的，用1111 1111 表示-1 还是 -127并没有什么原则问题

负数使用补码的好处是可以简化硬件实现，例如：

2 0000 0010

-2 1111 1110

二进制相加为零，可简化硬件实现

计算机中的速度与空间

1字节(Byte) = 8bit

宽带运营商标识网速的单位是Kbps或者Mbps(bit per second)这里是bit而不是Byte

所以1Mbps的下载速度下载100M大小的文件，需要800s而不是100s

bps->Kbps->Mbps->Gbps->Tbps

1Kbps=1000bps(其他依此类推)

Byte->KB->MB->GB->TB

1KB=1024B(其他依此类推)

我们通常更关注的实际真是的速度

实际速度会有三方面的因素影响：1、源文件的读取速度；2、传输速度；3、目的写入速度

100M的网络带宽是瓶颈，1000M的网络存储介质就是瓶颈了